
–ќ«ƒ≤Ћ 4
ѕ≤ƒ¬»ў≈ЌЌя ≈‘≈ “»¬Ќќ—“≤ ЅјЌ ≤¬—№ ќ√ќ ћј– ≈“»Ќ√” Ќј ќ—Ќќ¬≤ ћ≤—
4.1. —труктура ћ≤— та њњ першочергов≥ задач≥ в комерц≥йному банку
 |
–ќ«ƒ≤Ћ 4 ѕ≤ƒ¬»ў≈ЌЌя ≈‘≈ “»¬Ќќ—“≤ ЅјЌ ≤¬—№ ќ√ќ ћј– ≈“»Ќ√” Ќј ќ—Ќќ¬≤ ћ≤— 4.1. —труктура ћ≤— та њњ першочергов≥ задач≥ в комерц≥йному банку
|
≈коном≥чн≥ реал≥њ в ”крањн≥ поставили перед банками нов≥ задач≥, повТ¤зан≥ з перспективами њхнього розвитку: необх≥дн≥сть самост≥йноњ розробки маркетинговоњ концепц≥њ та стратег≥њ, оц≥нки на¤вних ресурс≥в ≥ впливу зовн≥шнього середовища. ÷е призводить до ≥стотного ускладненн¤ функц≥й управл≥нн¤ ≥ пошуку нових банк≥вських ≥нформац≥йних технолог≥й. —учасн≥ ≥нформац≥йн≥ технолог≥њ, що спри¤ють формуванню новоњ арх≥тектури обробки ≥нформац≥њ, дозвол¤ють банкам створювати принципово нов≥ ≥нформац≥йн≥ системи, що значно п≥двищують продуктивн≥сть њхньоњ д≥¤льност≥, вдосконалюють банк≥вськ≥й менеджмент.
як св≥дчить св≥товий досв≥д, сьогодн≥ багато кредитних ≥нститут≥в стикаютьс¤ з проблемою розвитку оновлених банк≥вських структур на основ≥ нов≥тньоњ ≥нформац≥йноњ технолог≥њ, вир≥шальним моментом ¤коњ Ї створенн¤ горизонтально ≥нтегрованих систем, структурованих за окремими сегментами (угоди з приватними ≥ корпоративними кл≥Їнтами, ≥нвестиц≥йна д≥¤льн≥сть та ≥н.). ¬ кожному сегмент≥ зд≥йснюЇтьс¤ окремий виробничий процес, що доповнюЇтьс¤ специф≥чними процесами обслуговуванн¤ ≥ управл≥нн¤. ƒл¤ кожного операц≥йного процесу сл≥д шукати найб≥льш виг≥дний проект прикладних р≥шень [188, с.47].
—творенн¤ ћ≤— в банках ”крањни маЇ зд≥йснюватис¤ на п≥дстав≥ методолог≥њ њхнього моделюванн¤ ≥ побудови з врахуванн¤м тенденц≥й сучасних ≥нформац≥йних технолог≥й та здобутк≥в заруб≥жноњ банк≥вськоњ практики у дан≥й сфер≥.
¬икористовуючи обрану нами в п≥дрозд≥л≥ 2.4. методику, що заснована на концепц≥њ системи, ¤ка враховуЇ зовн≥шнЇ середовище, ц≥лепокладанн¤ ≥ взаЇмов≥дносини ≥з середовищем в процес≥ њњ функц≥онуванн¤ ≥ розвитку, ћ≤— комерц≥йного банку можна зобразити у вигл¤д≥ графа ц≥лей ≥ функц≥й, що маЇ 8 р≥вн≥в декомпозиц≥њ (рис. 4.1.).
|
ѕерший р≥вень
ƒругий р≥вень
“рет≥й р≥вень „етвертий р≥вень ѕТ¤тий р≥вень
Ўостий р≥вень
—ьомий р≥вень |
|
–ис.4.1. √раф ц≥лей ≥ функц≥й ћ≤— банк≥в (загальний вигл¤д)
1.1. Ц забезпеченн¤ ефективного функц≥онуванн¤ ≥ розвитку комерц≥йних банк≥в; 2.1 Ц виживанн¤ банк≥в; 2.2 Ц завоюванн¤ частки ринку; 2l Ц м≥н≥м≥зац≥¤ витрат; 3.1 Ц макросередовище; 3.2 Ц п≥дв≥домч≥ системи; 3.3 Ц зовн≥шнЇ м≥кросередовище; 3.4 Ц власна система управл≥нн¤; 4.1 Ц 4.16 Ц види д≥¤льност≥ (табл.4.1); 5.1 Ц 5m Ц функц≥њ; 6.1 Ц 6n Ц задач≥; 7.1 Ц прийн¤тт¤ р≥шень; 7.2 Ц реал≥зац≥¤ р≥шень; 7.3 Ц контроль виконанн¤
ожному р≥вню в≥дпов≥даЇ етап структуризац≥њ, що реал≥зуЇ прийн¤ту концепц≥ю ћ≤— комерц≥йного банку. –озгл¤немо докладно кожний з цих етап≥в (р≥вн≥в).
Ќа першому р≥вн≥ зд≥йснюЇтьс¤ формуванн¤ глобальноњ мети системи. ћета найвищого р≥вн¤ в найб≥льш загальн≥й ≥ зручн≥й дл¤ декомпозиц≥й форм≥ маЇ описувати к≥нцевий результат, дл¤ дос¤гненн¤ ¤кого створюЇтьс¤ та ≥снуЇ система. “ому глобальну мету ћ≤— комерц≥йного банку можна визначити ¤к "«абезпеченн¤ ефективного функц≥онуванн¤ ≥ розвитку банку".
ƒругий р≥вень маЇ назву "ƒекомпозиц≥¤ за ознакою Д¬иди конкретних ц≥лей". ¬веденн¤ цього етапу Ї необх≥дним дл¤ б≥льшост≥ банк≥в, що прагнуть до конкретних ц≥лей, ¤к≥ конкретизують глобальну мету. ѕри вид≥ленн≥ такоњ системи ц≥лей необх≥дно дотримуватись таких загальносистемних умов:
- повнота (забезпеченн¤ дос¤гненн¤ ц≥лей верхнього р≥вн¤ ≥Їрарх≥њ);
- м≥н≥мальн≥сть (обмежений наб≥р ц≥лей);
- операц≥йн≥сть (ч≥тк≥сть ≥ одночасн≥сть формулюванн¤ ц≥лей);
- можлив≥сть проведенн¤ декомпозиц≥њ.
як показали досл≥дженн¤, на практиц≥ найпоширен≥шими Ї так≥ конкретн≥ ц≥л≥, що сто¤ть перед банками: забезпеченн¤ виживанн¤ банку, завоюванн¤ м≥цних позиц≥й на ц≥льовому ринку, зб≥льшенн¤ частки ринку банку, максим≥зац≥¤ прибутку, м≥н≥м≥зац≥¤ витрат при збереженн≥ частки ринку, завоюванн¤ л≥дерства за ¤к≥стю банк≥вського продукту.
ћожуть формуватис¤ й ≥нш≥ ц≥л≥, або може ставитис¤ дек≥лька конкретних ц≥лей, причому кожна мета може описуватись у вигл¤д≥ економ≥ко-математичноњ модел≥.
Ќаприклад, мета "ћаксим≥зац≥¤ прибутку за пер≥од “ " може бути задана у вигл¤д≥:
—(х)=![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
![]() ,
≥=1,Е,m
(4.3)
,
≥=1,Е,m
(4.3)
aj![]() bj
, j=1,Е, n,
(4.4)
bj
, j=1,Е, n,
(4.4)
де —(х) - сумарний прибуток банку;
pj Ц прибуток в≥д реал≥зац≥њ одиниц≥ j-го продукту, гр. од.;
xj Ц к≥льк≥сть банк≥вських продукт≥в j-го виду;
Q Ц м≥стк≥сть ринку в пер≥од “, гр. од.;
cj Ц ц≥на одиниц≥ продукту j-го виду, гр. од.;
d Ц частка ринку банк≥вських продукт≥в, що плануЇтьс¤, %;
aij Ц норма витрат ≥-го ресурсу на виробництво одиниц≥ j-го продукту;
Ri Ц на¤вн≥сть ≥-го ресурсу;
n Ц к≥льк≥сть вид≥в банк≥вських продукт≥в, що реал≥зуютьс¤;
m Ц к≥льк≥сть вид≥в ресурс≥в, що враховуютьс¤ в модел≥;
aj Ц нижн¤ межа реал≥зац≥њ j-го продукту, тобто к≥льк≥сть, ¤ка необх≥дна дл¤ збереженн¤ частки ринку по j-му продукту, що визначаЇтьс¤ маркетинговими досл≥дженн¤ми;
bj Ц верхн¤ межа реал≥зац≥њ j-го продукту, що визначаЇтьс¤ споживчим попитом на банк≥вський продукт j-го виду.
” дан≥й модел≥ (4.1) - ц≥льова функц≥¤ —(х) - сумарний прибуток банку, (4.2) - вимоги щодо забезпеченн¤ частки ринку банк≥вських продукт≥в, (4.3) - обмеженн¤ щодо ресурс≥в, (4.4) - обмеженн¤ на виробництво банк≥вського продукту, що накладаЇтьс¤ маркетинговим досл≥дженн¤м
Ќадамо у вигл¤д≥ економ≥ко-математичноњ модел≥ ще одну межу Ц зб≥льшенн¤ частки ринку. ÷≥льова функц≥¤ —(х) буде мати вигл¤д
C(х)=![]()
![]() ,
i
=1,Е, m
,
i
=1,Е, m
xj![]() aj
, j=1,Е,
n
aj
, j=1,Е,
n
ј мету Д«авоюванн¤ л≥дерства за "¤к≥стю банк≥вського продукту", ¤ка на сьогодн≥шн≥й день у практиц≥ заруб≥жних банк≥в Ї одн≥Їю з найб≥льш важливих, можна описати таким чином. ÷≥льова функц≥¤ (р) Ц комплексний показник ¤кост≥:
(р)=![]()
pimin![]() pi
pi![]() pimax
, i=1,Е,
n
pimax
, i=1,Е,
n
![]() =A,
=A,
де pi Ц значенн¤ ≥-го показника ¤кост≥ (в≥дносна величина);
а≥ Ц ваговий коеф≥ц≥Їнт ≥-го показника ¤кост≥;
pimin, pimax - в≥дпов≥дно нижн¤ ≥ верхн¤ межа можливоњ зм≥ни ≥-го показника ¤кост≥;
fi(pi) Ц функц≥¤ витрат на забезпеченн¤ значенн¤ ≥-го показника ¤кост≥;
ј Ц верхн¤ межа кошт≥в, що вид≥л¤ютьс¤ дл¤ забезпеченн¤ найкращих ≥з можливих показник≥в ¤кост≥.
«розум≥ло, що можуть бути побудован≥ й ≥нш≥, б≥льш детал≥зован≥ модел≥, в тому числ≥ й дл¤ конкретного виду банк≥вського продукту. ¬с≥ ц≥ модел≥ описують конкретн≥ ц≥л≥ комерц≥йного банку.
Ќа третьому р≥вн≥ зд≥йснюЇтьс¤ декомпозиц≥¤ за ознакою "ѕрост≥р ≥н≥ц≥юванн¤ ц≥лей". ÷ей етап повТ¤заний ≥з формуванн¤м п≥дц≥лей досл≥джуваноњ системи, що ≥н≥ц≥юютьс¤ вимогами ≥ потребами систем оточуючого середовища. ¬с≥ системи, що зд≥йснюють вплив на формуванн¤ п≥дц≥лей створюваноњ ћ≤— банк≥в, ми под≥л¤Їмо на чотири класи (рис.4.2):
1. ћакросередовище Ц охоплюЇ обТЇктивн≥ фактори, що формують обовТ¤зков≥ вимоги до системи (наприклад, сплата податк≥в, обовТ¤зков≥ нормативи).
2. ѕ≥дв≥домч≥ системи Ц формують вимоги, ¤к≥ виступають загалом ¤к ресурсн≥ обмеженн¤.
3. «овн≥шнЇ м≥кросередовище.
4. —ама досл≥джувана система, ¤ка завжди кр≥м глобальноњ мети маЇ внутр≥шн≥ потреби самовдосконаленн¤.
„етвертий р≥вень Ц декомпозиц≥¤ за ознакою "¬иди д≥¤льност≥". Ќа цьому етап≥ визначаютьс¤ вс≥ види д≥¤льност≥, ¤к≥ охоплюЇ ћ≤—, що проектуЇтьс¤, ≥ котр≥ забезпечують дос¤гненн¤ вище викладених п≥дц≥лей, що ≥н≥ц≥юютьс¤ в≥дпов≥дною системою верхнього р≥вн¤ (табл.4.1).
≈тапи пТ¤тий та шостий Ц декомпозиц≥¤ за ознаками "‘ункц≥њ" та "«адач≥ управл≥нн¤". Ќа цих р≥вн¤х формуютьс¤ функц≥њ ≥ задач≥, що вход¤ть у ћ≤—, дл¤ кожного виду д≥¤льност≥. ѓхнЇ виконанн¤ або вир≥шенн¤ забезпечуЇ дос¤гненн¤ конкретних оперативних ц≥лей ≥ нараз≥ глобальноњ мети системи. ƒаний етап Ї найб≥льш специф≥чним дл¤ кожного конкретного банку, хоча Ї певне перехрещенн¤
|
ћакросередовище |
|
1. ≈коном≥чн≥ фактори 2. ѕол≥тико-правов≥ фактори 3. —оц≥ально-культурн≥ фактори 4. ѕриродн≥ фактори 5. Ќауково-техн≥чн≥ фактори 6. ƒемограф≥чн≥ фактори |
![]()
|
¬ласна система управл≥нн¤ (ћ≤—) |
|
«овн≥шнЇ м≥кросередовище |
|
1. ÷≥л≥ ≥ прогнозуванн¤ розвитку ≥ плануванн¤ д≥¤льност≥ банк≥в 2.
«м≥ст ≥ форми: розробка
орган≥зац≥йно-функц≥ональноњ
структури
3. ћетоди: система нормативно-методичного забезпеченн¤ |
1. л≥Їнти 2. онкуренти 3. ѕостачальники 4. ѕосередники 5. онтактн≥ аудитор≥њ |
![]()
![]()
|
ѕодв≥домча система (ресурсне забезпеченн¤) |
|
1. адри 2. Ќауково-техн≥чний потенц≥ал 3. ћатер≥ально-техн≥чна база 4. ‘≥нансове забезпеченн¤ 5. ≤нформац≥йне забезпеченн¤ |
–ис.4.2. —хема простору ≥н≥ц≥юванн¤ ц≥лей у ћ≤— комерц≥йного банку
“аблиц¤ 4.1
¬иди д≥¤льност≥, що ≥н≥ц≥юютьс¤ навколишн≥м простором у ћ≤— банку
|
ѕрост≥р ≥н≥ц≥юванн¤ ц≥лей |
ќсновн≥ види д≥¤льност≥ |
| 1. ¬заЇмод≥¤ з макросередовищем |
1.1. јнал≥з макроеконом≥чних показник≥в розвитку економ≥ки. 1.2. јнал≥з нееконом≥чних показник≥в. ќц≥нка ≥ анал≥з конкурентного середовища. |
| 2. «абезпеченн¤ д≥¤льност≥ п≥дв≥домчоњ системи |
1.3. –озробка ≥ реал≥зац≥¤ б≥знес-план≥в розвитку банку. 1.4. ‘ормуванн¤ ресурс≥в банку. 1.5. ћатер≥ально-техн≥чне забезпеченн¤. 1.6. ¬иробництво банк≥вських продукт≥в. 1.7. «абезпеченн¤ ф≥нансовими ресурсами. |
|
3. «абезпеченн¤ взаЇмод≥њ ≥з зовн≥шн≥м м≥кросередовищем |
1.8. ƒосл≥дженн¤ попиту ≥ пропозиц≥њ 1.9. ƒосл≥дженн¤ конкурент≥в 1.10. —творенн¤ ц≥льового ринку, включаючи його сегментуванн¤ 1.11. ‘ормуванн¤ продуктовоњ ≥ ц≥новоњ пол≥тики 1.12. ќрган≥зац≥¤ ≥ стимулюванн¤ збуту банк≥вських продукт≥в 1.13. ќц≥нка ≥ анал≥з ф≥нансового стану позичальник≥в |
|
4. ¬досконаленн¤ власноњ системи управл≥нн¤ |
1.14. –озробка сучасноњ орган≥зац≥йно-функц≥ональноњ структрури 1.15. ¬досконаленн¤ нормативно-методичного забезпеченн¤ 1.16. —творенн¤ сучасних ≥нформац≥йних систем |
основних функц≥й ≥ задач.
–≥вень сьомий Ц декомпозиц≥¤ за ознакою Ђ÷икл управл≥нн¤ї, ¤ка подана трьома блоками: прийн¤тт¤ р≥шень (прогнозуванн¤, плануванн¤); реал≥зац≥¤ р≥шень (орган≥зац≥¤, координац≥¤ ≥ регулюванн¤, актив≥зац≥¤ ≥ стимулюванн¤); контроль виконанн¤ (обл≥к ≥ анал≥з).
¬осьмий р≥вень Ц декомпозиц≥¤ за ознакою "ƒелегуванн¤ повноважень" Ц необх≥дний дл¤ ч≥ткого функц≥онуванн¤ досл≥джуваноњ системи. ƒана ознака структурована за такими складовими: комплексна п≥дготовка р≥шень; участь у п≥дготовц≥ р≥шень; узгодженн¤ на стад≥њ п≥дготовки р≥шень; прийн¤тт¤ р≥шень; виконанн¤ р≥шень; контроль виконанн¤. ÷ей етап в≥дсутн≥й на рис.4.2., але в≥н Ї необх≥дним при закр≥пленн≥ функц≥й (задач) за структурними п≥дрозд≥лами банку.
“аким чином, використовуючи вище розгл¤нуту методику, можна отримати повний перел≥к задач ћ≤— дл¤ кожного комерц≥йного банку.
¬ залежност≥ в≥д конкретних умов будь-¤кого комерц≥йного банку з повного перел≥ку вид≥в д≥¤льност≥, функц≥й ≥ задач управл≥нн¤ маркетингом у склад≥ ћ≤— необх≥дно в≥д≥брати т≥, що дозвол¤ють дос¤гти глобальноњ мети з найменшими витратами, або за на¤вних ресурс≥в дають можлив≥сть отримати найб≥льш значущ≥ результати в дос¤гненн≥ мети.
” п≥дрозд≥л≥ 2.4. нами було запропоноване три групи метод≥в вир≥шенн¤ ц≥Їњ проблеми: оптим≥зац≥йн≥, експертн≥ та евристичн≥. «г≥дно з прийн¤тою вище структурою ћ≤— (рис.4.1.) доц≥льним Ї використанн¤ одного з експертних метод≥в Ц методу розвТ¤зувальних матриць. ƒл¤ цього подамо зображенн¤ на рис.4.1. у зручному дл¤ застосуванн¤ зазначеного методу вигл¤д≥ (рис.4.3.). Ћ≥терами а, в, с, d, f позначен≥ в≥дносна вага елемент≥в в≥дпов≥дного р≥вн¤, а ≥ндексами при л≥терах - пор¤дковий номер елемента на даному р≥вн≥. Ќасамперед, до початку застосуванн¤ методу розвТ¤зувальних матриць, з множини можливих конкретних ц≥лей обираютьс¤ саме т≥, котр≥ ставить перед собою кер≥вництво банку. ¬с≥ ≥нш≥ елементи графа ц≥лей ≥ функц≥й або п≥дл¤гають попередньому в≥дбору з врахуванн¤м конкретних умов банку, або н≥, тобто њх можна прийн¤ти до експертизи в тому вигл¤д≥, в ¤кому вони подан≥ на рис.4.3.

¬≥дносна
вага
за вс≥ма р≥вн¤ми маЇ бути нормована. ѕри
цьому дл¤ зручност≥ опитуванн¤
експерт≥в в≥дносна вага визначаЇтьс¤ не в
частках одиниц≥, а у в≥дсотках, тобто
нормуЇтьс¤ по в≥дношенню до 100:
![]() =100 Ќа
першому етап≥ експертом установлюЇтьс¤
в≥дносна вага конкретних ц≥лей, а в≥дносна
вага ≥нших обраховуЇтьс¤ за формулами (4.5),
(4.6), (4.7). Ќа другому етап≥ експерт оц≥нюЇ
внесок кожного п≥дпростору простору
≥н≥ц≥юванн¤ ц≥лей (макросередовища,
зовн≥шнього м≥кросередовища, власноњ
системи управл≥нн¤, п≥дв≥домчоњ системи) до
реал≥зац≥њ конкретних ц≥лей, що лежать на
вищому р≥вн≥, у вигл¤д≥ в≥дносноњ оц≥нки gij(1).
«розум≥ло, що в≥дносн≥ оц≥нки мають бути
нормован≥:
=100 Ќа
першому етап≥ експертом установлюЇтьс¤
в≥дносна вага конкретних ц≥лей, а в≥дносна
вага ≥нших обраховуЇтьс¤ за формулами (4.5),
(4.6), (4.7). Ќа другому етап≥ експерт оц≥нюЇ
внесок кожного п≥дпростору простору
≥н≥ц≥юванн¤ ц≥лей (макросередовища,
зовн≥шнього м≥кросередовища, власноњ
системи управл≥нн¤, п≥дв≥домчоњ системи) до
реал≥зац≥њ конкретних ц≥лей, що лежать на
вищому р≥вн≥, у вигл¤д≥ в≥дносноњ оц≥нки gij(1).
«розум≥ло, що в≥дносн≥ оц≥нки мають бути
нормован≥:
![]() = 100, ≥=1,Е, N1
= 100, ≥=1,Е, N1
¬ результат≥ отримуЇмо розвТ¤зувальну матрицю G(1):
G(1)
=
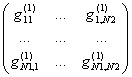
ƒал≥ розрахувуютьс¤ в≥дносн≥ ваги елемент≥в простору ≥н≥ц≥юванн¤ ц≥лей bj за формулою:
bj
=
![]() ,
j=1, Е, N2
(4.5)
,
j=1, Е, N2
(4.5)
Ќа
третьому етап≥, знаючи bj
≥
побудувавши аналог≥чним чином розвТ¤зувальну
матрицю G(2)
, в ¤к≥й також
![]() ,
,
обчислюютьс¤ в≥дносн≥ ваги вид≥в д≥¤льност≥ cj:
cj=
![]() ,
j=1,
Е, N3
,
j=1,
Е, N3
(4.6)
,
j=1,
Е, N3
,
j=1,
Е, N3
(4.6)
ѕродовжуючи на наступних етапах таким же чином, зрештою за формулою, аналог≥чною (4.6) розраховуютьс¤ в≥дносн≥ ваги задач управл≥нн¤ ћ≤—:
fj =
ћаючи оц≥нки в≥дносноњ важливост≥ задач управл≥нн¤ ћ≤—, њх можна використовувати при ранжуванн≥ задач або при побудов≥ конкретних економ≥ко-математичних моделей.
«астосуЇмо ≥нтегральний метод
ранжуванн¤ задач (функц≥й). Ќехай Ї n
задач маркетинга: f1,
f2,
Е, fn
,
¤к≥ необх≥дно впор¤дкувати за спаданн¤м
њхньоњ значущост≥. “а нехай попередньо будь-¤кими
експертними методами кожн≥й задач≥
присвоЇно
оц≥нку:
або ранг, або абсолютну
(в≥дносну)
оц≥нку
задач≥. “аким чином, ¤кщо застосовувалось m
метод≥в, то маЇмо m
впор¤дкованих по м≥р≥ спаданн¤
посл≥довностей оц≥нки задач
![]() , де де
k=
, де де
k=![]() ; i=
; i=
![]() .
.
ўоб застосувати даний метод, необх≥дно ц≥ вс≥ посл≥довност≥ нормал≥зувати, використовуючи формулу:
![]() (4.8)
,
(4.8)
,
де
![]() - нормал≥зована
оц≥нка k-њ
задач≥ при застосуванн≥ ≥-го
методу;
- нормал≥зована
оц≥нка k-њ
задач≥ при застосуванн≥ ≥-го
методу;
![]() - м≥н≥мальне
значенн¤ оц≥нки в посл≥довност≥ оц≥нок
задач, отриманих ≥-м
методом;
- м≥н≥мальне
значенн¤ оц≥нки в посл≥довност≥ оц≥нок
задач, отриманих ≥-м
методом;
![]() - максимальне значенн¤ оц≥нки в
посл≥довност≥ оц≥нок задач, отриманих ≥-м
методом.
- максимальне значенн¤ оц≥нки в
посл≥довност≥ оц≥нок задач, отриманих ≥-м
методом.
ƒал≥ обчислюЇтьс¤ ≥нтегральний показник (рк) кожноњ k-њ задач≥ у вигл¤д≥ л≥н≥йноњ згортки:
рк =
![]() , k
=
, k
=
![]() ,
(4.9),
,
(4.9),
де
![]() , 0<
, 0<
![]() <1,
<1,
![]() -
питома вага ≥-го
метода вибору.
-
питома вага ≥-го
метода вибору.
якщо припустити, що вс≥ методи Ї
р≥внозначними, то
![]() .
¬иконавши сортуванн¤ посл≥довност≥ {pk}k=1,
Е, n
в
пор¤дку спаданн¤,
отримаемо ранжовану посл≥довн≥сть задач
ћ≤—, на початку ¤коњ будуть сто¤ти т≥ задач≥
(функц≥њ), котр≥ необх≥дно
включити до
системи (автоматизувати) в першу чергу.
.
¬иконавши сортуванн¤ посл≥довност≥ {pk}k=1,
Е, n
в
пор¤дку спаданн¤,
отримаемо ранжовану посл≥довн≥сть задач
ћ≤—, на початку ¤коњ будуть сто¤ти т≥ задач≥
(функц≥њ), котр≥ необх≥дно
включити до
системи (автоматизувати) в першу чергу.
–озгл¤немо сутн≥сть експертних метод≥в дл¤ оц≥нки задач (функц≥й) ћ≤— комерц≥йного банку та обробку результат≥в експертизи ≥нтегральним методом ранжуванн¤ функц≥й.
ѕерший метод Ц м≥н≥м≥зац≥й в≥дхилень м≥ж перевагами групи експерт≥в та ≥ндив≥дуальними р≥шенн¤ми.
Ќехай Ї m експерт≥в та n задач (функц≥й) управл≥нн¤ ћ≤—. ожний експерт оц≥нюЇ задач≥ управл≥нн¤ за допомогою n-вим≥рноњ системи оц≥нок: найб≥льш значима (важлива) задача отримуЇ n бал≥в, найменш значима в перел≥ку задач ћ≤— отримуЇ 1 бал [189]. ≤ндив≥дуальн≥ переваги вигл¤дають так, ¤к показано в табл.4.2,
“аблиц¤ 4.2
≤ндив≥дуальн≥ переваги задач управл≥нн¤ ћ≤—
| «адач≥ управл≥нн¤ ћ≤— |
ќц≥нки в балах |
|||
|
1-й експерт |
2-й експерт |
Е |
m-й експерт |
|
|
1 |
а11 |
а12 |
Е |
a1m |
| Е | Е | Е | Е | Е |
|
n |
an1 |
an2 | Е | anm |
де aij Ц к≥льк≥сть бал≥в, присвоЇних ≥-т≥й задач≥ j-м експертом, ≥=1, Е, m.
ƒл¤ того, щоб м≥н≥м≥зувати на¤вн≥ в≥дхиленн¤ оц≥нок член≥в експертноњ групи в≥д групового р≥шенн¤, будуЇтьс¤ матриц¤ розб≥жностей результат≥в р≥шенн¤ (табл.4.3)
“аблиц¤ 4.3
ћатриц¤ розб≥жностей оц≥нок експерт≥в
|
√рупов≥ р≥шенн¤ |
–≥зниц¤ оц≥нок |
ћаксимальна розб≥жн≥сть |
||
|
1-й експерт |
Е |
m-й експерт |
||
|
1 |
n-a11 |
Е |
n-a1m |
Max {n-aij} 1
|
|
Е |
Е |
Е |
Е |
Е |
|
n |
n-an1 |
Е |
n-anm |
Max {n-anj} 1
|
ѕри цьому спочатку зд≥йснюютьс¤ пропозиц≥њ про пр≥оритетний виб≥р групою т≥Їњ або ≥ншоњ задач≥ управл≥нн¤, а пот≥м оц≥нюютьс¤ розб≥жност≥ м≥ж цим груповим та ≥ндив≥дуальними р≥шенн¤ми.
ƒал≥ в р¤дках матриц≥ (таблиц≥) дл¤
кожноњ задач≥ знаходитьс¤ максимальна
розб≥жн≥сть, ¤ка записуЇтьс¤ в останню
графу табл.4.3. ѕот≥м з цих максимальних
розб≥жностей обираЇтьс¤ найменша, тобто е1=
![]() .
.
«адача
з номером n1,
що в≥дпов≥даЇ величин≥ е1,
пос≥даЇ перше м≥сце в перел≥ку задач
управл≥нн¤, що п≥дл¤гають автоматизац≥њ в
склад≥ ћ≤—, а пот≥м вона виключаЇтьс¤ з
подальшого розгл¤ду. ѕот≥м обчислюЇтьс¤
величина е2=
![]() {n
- aij}.
{n
- aij}.
«адача з номером n2, що в≥дпов≥даЇ величин≥ е2, пос≥даЇ друге м≥сце в ранжованому перел≥ку задач ћ≤—. јналог≥чно процедура продовжуЇтьс¤ доти, поки не будуть впор¤дкован≥ зг≥дно з прийн¤тим критер≥Їм вс≥ задач≥ управл≥нн¤ ћ≤—.
ƒругий експертний метод Ц метод мед≥ани емен≥. ќдним з основних математичних пон¤ть, що використовують при анал≥з≥ ≥ обробц≥ експертноњ ≥нформац≥њ, Ї в≥дношенн¤. ≤нформац≥¤ про в≥дношенн¤ може бути подана р≥зними способами [162]. ¬≥дношенн¤ можна задавати безпосередн≥м перерахуванн¤м пар елемент≥в множини ј. ѕроте б≥льш зручним Ї матричний спос≥б поданн¤ ≥нформац≥њ про в≥дношенн¤. —товпчики ≥ р¤дки матриц≥ || pij || в≥дношенн¤ p позначатимемо також через ћ(–). ƒл¤ поданн¤ в≥дношень л≥н≥йного пор¤дку використовуЇтьс¤ матриц¤ || pij || з елементами:
Pij
= ![]()

“ак≥ матриц≥ в≥дношень Ї антисиметричними, тобто pij = - pij , i, j Î{1, Е, n}.
ќск≥льки оц≥нки експерт≥в мають ¤к≥сний характер, припустимо, що кожним експертом встановлено в≥дношенн¤ л≥н≥йного або часткового пор¤дку дл¤ сукупност≥ функц≥й {a1, a2, Е, an}, що розгл¤даютьс¤. ƒл¤ m експерт≥в маЇмо m в≥дношень P1, P2, Е, Pm , де j-те в≥дношенн¤ зображене вектором
Pj
=
![]() , j =
1, Е, n.
, j =
1, Е, n.
ќдним
з основних ≥нструмент≥в, що
використовуютьс¤ п≥д час анал≥зу ≥ обробки
експертноњ ≥нформац≥њ, Ї м≥ри близькост≥,
¤к≥ дозвол¤ють визначити, наск≥льки
близькими чи далекими Ї точки зору
експерт≥в. ’арактерною особлив≥стю м≥р
близькост≥ Ї акс≥оматичний спос≥б њхнього
введенн¤. ћ≥ра близькост≥ повн≥стю
визначаЇтьс¤ сукупн≥стю вимог, ¤к≥ вона маЇ
задовольн¤ти. «окрема, м≥ра близькост≥ м≥ж
дов≥льними ранжуванн¤ми P1,
P2,
що задовольн¤Ї систему аксиом [165, c.39-43],
визначаЇтьс¤ за формулою d
( P1,
P2
) = 0,5
![]()
« уведенн¤м м≥р близькост≥ Ї можлив≥сть визначити в≥дстань м≥ж дов≥льною парою ранжувань. «розум≥лим буде припустити, що результуюче ранжуванн¤
F(P1, Е, Pm) маЇ бути розташованим щонайближче до ранжувань P1, Е, Pm. “аке ранжуванн¤ ћ0(P1, Е, Pm) називаЇтьс¤ мед≥аноњ емен≥ ≥ визначаЇтьс¤ виразом:
ћ0(P1,
Е, Pm) = arg min
![]()
≤снують евристичн≥ ≥ комб≥наторн≥ алгоритми обчисленн¤ мед≥ани емен≥. ћи розгл¤немо задачу знаходженн¤ мед≥ани емен≥ на множин≥ вектор≥в переваг.
якщо – Ц дов≥льне ранжуванн¤, ≥ матриц¤ в≥дношень ћ(–) вм≥щуЇ елементи aij виду
1, ¤кщо ai > aj
aij
= ![]() 0,
¤кщо ai
ї
aj
0,
¤кщо ai
ї
aj
-1, ¤кщо ai < aj,
то вектор переваг π =( π 1, Е, π n) визначаЇтьс¤ так:
π≥ =
![]()
ќтже, ≥-та координата вектора переваг показуЇ, ск≥льки функц≥й (задач) перевищують за значим≥стю ≥-ту функц≥ю (задачу).
Ќехай π(1), Е, π(m) Ц вектори переваг, задан≥ експертами, а – Ц дов≥льне ранжуванн¤. Ќадамо йому у в≥дпов≥дн≥сть n - вим≥рний вектор π =( π1, π2, Е, πn), ≥-та компонента ¤кого дор≥внюЇ к≥лькост≥ функц≥й, що переважають а≥. ћед≥аною емен≥ в даному випадку буде ранжуванн¤ π0 таке, що
![]() ,
(4.10)
,
(4.10)
¬
(4.10) м≥н≥мум беретьс¤ за вс≥ма векторами
переваг. «≥ сп≥вв≥дношенн¤ (4.10) випливаЇ, що ![]()
ѕрипустимо,
що в ранжуванн≥ – функц≥¤ а≥
розташована на j-му
м≥сц≥. ¬ведемо величину rij
=
![]() .
.
–озгл¤даючи ранжуванн¤, в ¤ких дов≥льна функц≥¤ а≥, jÎ{1, Е, n}, розташована посл≥довно в≥д 1-го до n- го м≥сц¤, отримаЇмо матрицю втрат || rij ||. ” даном випадку елемент rij характеризуЇ "незгоду" експерт≥в з призначенн¤м функц≥њ (задач≥) а≥ на j-те м≥сце в результуючому ранжуванн≥. ¬ведемо зм≥нн≥
xij
=

¬ектор х = (х11, х12, Е, хnm) в≥дпов≥даЇ певному ранжуванню, коли
![]() ,
i=1,
Е, n;
,
i=1,
Е, n;
![]() , j=1, Е,
n.
, j=1, Е,
n.
ћед≥аною
емен≥ буде ранжуванн¤, при ¤кому
![]() дос¤гаЇ м≥н≥мума.
ќтже, задача знаходженн¤ мед≥ани
дос¤гаЇ м≥н≥мума.
ќтже, задача знаходженн¤ мед≥ани
емен≥ може бути сформульована у вигл¤д≥ задач≥ про виб≥р або задач≥ про призначенн¤:
—(х) =
![]()
![]() min
(4.11)
min
(4.11)
при обмеженн¤х:
![]() , i=1,
Е, n
(4.12)
, i=1,
Е, n
(4.12)
![]() , j=1, Е, n
(4.13)
, j=1, Е, n
(4.13)
хij
= ![]() i,
j= 1,Е, n
(4.14)
i,
j= 1,Е, n
(4.14)
“аким чином, при використанн≥ м≥ри близькост≥ м≥ж векторами переваг мед≥ана емен≥ знаходитьс¤ досить ефективно. ƒане ранжуванн¤ визначаЇ пр≥оритет функц≥й (задач) у склад≥ ћ≤—.
≤стотно новим моментом при застосуванн≥ даного методу служить вимога щодо доц≥льност≥ виокремленн¤ чотирьох клас≥в функц≥й ћ≤—, кожний з ¤ких в≥дпов≥даЇ простору ≥н≥ц≥юванн¤ ц≥лей, а пот≥м посл≥довне застосуванн¤ метода мед≥ани емен≥ до кожного класу окремо. ¬ результат≥ маЇмо чотири посл≥довност≥ проранжованих функц≥й, з котрих зрештою формуЇтьс¤ функц≥ональна частина ћ≤— за критер≥¤ми найб≥льшоњ значущост≥ та ≥нформац≥йного взаЇмозвТ¤зку функц≥й (задач) управл≥нн¤ з врахуванн¤м на¤вних ресурс≥в. якщо ж певн≥ класи функц≥й не ц≥кавл¤ть кер≥вник≥в банку в даний момент часу, то вони можуть ≥ не розгл¤датис¤.
ѕоширеним способом оц≥нки складових структур ц≥лей ≥ функц≥й орган≥зац≥йно-економ≥чних систем Ї оц≥нка њхньоњ в≥дносноњ важливост≥ методом нормуванн¤ з використанн¤м дек≥лькох критер≥Їв та њхн≥х вагових коеф≥ц≥Їнт≥в. ≈кспертам пропонуЇтьс¤ оц≥нювати кожну функц≥ю за 10 Ц бальною або 100 Ц бальною шкалою, а пот≥м отриман≥ оц≥нки нормал≥зувати.
Ѕальн≥ оц≥нки мають зм≥ст пром≥жних м≥ж ранжуванн¤м ≥ к≥льк≥сним показником. “ому анал≥з бальних оц≥нок можна зд≥йснювати ¤к "к≥льк≥сними", так ≥ "¤к≥сними" методами. Ќа думку багатьох автор≥в доц≥льно обробл¤ти бальн≥ оц≥нки методами обох тип≥в [163, c.163]. —п≥впаданн¤ висновк≥в, отриманих урезультат≥ застосуванн¤ двох р≥зних п≥дход≥в,дозвол¤Ї скласти думку, що ц≥ висновки Ї обТЇктивними, а не виход¤ть з метод≥в обробки експертноњ ≥нформац≥њ.
ќтже, нехай задано наб≥р n функц≥й (задач) ћ≤—, ¤к≥ оц≥нюють за 100-бальною шкалою m експерт≥в. ѕроцедура оц≥нки функц≥й з врахуванн¤м компетентност≥ експерт≥в та њхньоњ подженост≥ охоплюЇ наступн≥ етапи:
1.
–озрахунок суми оц≥нок важливост≥ вс≥х
функц≥й, що надан≥ j-м
експертом:
Sj
=![]() ,
j=1,
Е, m
, де Sij
Ц оц≥нка важливост≥
,
j=1,
Е, m
, де Sij
Ц оц≥нка важливост≥
≥-оњ функц≥њ j-м експертом.
2.
ќбчисленн¤ в≥дносних оц≥нок важливост≥
≥-тоњ функц≥њ за
висновками j-го
експерта: Sij
= ![]() ,
≥=1, Е, n,
j=1,
Е,
,
≥=1, Е, n,
j=1,
Е,
3. ќц≥нка компетентност≥ експерт≥в
3.1. Ѕальна оц≥нка експерт≥в особою, що приймаЇ р≥шенн¤ ≥ Ї в≥дпов≥дальною за проведенн¤ експертизи. ќсоба, що приймаЇ р≥шенн¤, оц≥нюЇ кожного експерта за 5-бальною або 10-бальною шкалою з точки зору таких критер≥њв ¤к по≥нформован≥сть, квал≥ф≥кац≥¤, посада, що об≥ймаЇтьс¤, обТЇктивн≥сть, стаж роботи.
3.1.1.
ќбчисленн¤ суми оц≥нок j-го
експерта за вс≥ма критер≥¤ми
компетентност≥ (Mj):
Mj
= ![]() j=1,
Е, m
, де ћjl
Ц
j=1,
Е, m
, де ћjl
Ц
. оц≥нка j-го експерта за l-м критер≥Їм компетентност≥; L Ц к≥льк≥сть критер≥њв компетентност≥.
3.1.2.
ќбчисленн¤ суми оц≥нок компетентност≥
експерт≥в (ћ): ћ
= ![]()
3.1.3. –озрахунок в≥дносноњ оц≥нки компетентност≥ j-го експерта:
qj = ![]() ,
j=1, Е, m
(4.15)
,
j=1, Е, m
(4.15)
3.2. ќц≥нка компетентност≥, заснована на взаЇмооц≥нках експерт≥в [191].
Ќехай bkj Ц бальна оц≥нка компетентност≥ k-го експерта, надана j-м експертом. ¬загал≥ bkj може виражати частку випадк≥в, коли k -й експерт перемагав у суперечц≥ j-го, або к≥льк≥сть експерт≥в, що вважаЇ k -го компетентн≥шим за j-го тощо. “од≥ маЇмо матрицю ¬=(bij), i=1, Е, n, j=1, Е, m. ¬ектор q=(q1,q2, Е, qm) Ц вектор коеф≥ц≥Їнт≥в компетентност≥ експерт≥в. ѕозначимо qo =(1, 1, Е, 1) Ц m - вим≥рний вектор. ѕроцес розрахунку коеф≥ц≥Їнт≥в компетентност≥ qj пол¤гаЇ в посл≥довному застосуванн≥ перетворенн¤, що задаЇтьс¤ матрицею ¬, до початкового вектора qo [166]: qt = Bqt-1. ƒана формула може бути записана у вигл¤д≥: qt = Btq . ћатриц¤ ¬ Ї такою, що розкладаЇтьс¤, ¤кщо множину ≥ндекс≥в ћ={1, Е, m} можна розбити на дв≥ п≥дмножини ≤1 та ≤2 таким чином, що bkj=0 дл¤ вс≥х k Î ≤L, j Î I2. –озкладанн¤ матриц≥ ¬ означаЇ, що вс≥ експерти з ≤2 вважають некомпетентними вс≥х експерт≥в з ≤1.
Ѕудь-¤кий вектор q, що не
зм≥нюЇ "напр¤м" в результат≥
застосуванн¤ матриц≥ ¬, тобто задовольн¤Ї
р≥вн≥сть Bq=![]() q,
де
q,
де ![]() -
де¤ке число, називаЇтьс¤ власним вектором
матриц≥ ¬, а коеф≥ц≥Їнт "розт¤гненн¤"
-
де¤ке число, називаЇтьс¤ власним вектором
матриц≥ ¬, а коеф≥ц≥Їнт "розт¤гненн¤" ![]() -
власним числом, ¤кому в≥дпов≥даЇ q. якщо B не
розкладаЇтьс¤, тод≥:
-
власним числом, ¤кому в≥дпов≥даЇ q. якщо B не
розкладаЇтьс¤, тод≥:
q1в≥дп
= ![]() Bqt-1
, t
=1, 2, 3, Е
(4.16)
Bqt-1
, t
=1, 2, 3, Е
(4.16)
де ![]() =
=
![]() -
сума компонент вектора Bqt-1
, так що qt
Ц вектор
в≥дносних величин q
-
сума компонент вектора Bqt-1
, так що qt
Ц вектор
в≥дносних величин q![]() .
.
якщо
перейти до границ≥, тод≥
![]() Ї
максимальним власним числом матриц≥ ¬ з
в≥дпов≥дним власним
вектором
q
=
Ї
максимальним власним числом матриц≥ ¬ з
в≥дпов≥дним власним
вектором
q
=
![]() .
.
.
.
“аким чином, розрахунки можна зд≥йснювати за формулами:
![]() ,
,
qtв≥дн![]() =
=

Ќаведен≥ властивост≥ нев≥дТЇмних матриць довод¤ть, що процес обчисленн¤ коеф≥ц≥Їнт≥в компетентност≥ qj обовТ¤зково зб≥гаЇтьс¤ до власного вектора ¬, ¤кщо матриц¤ ¬ Ї такою, що не розкладаЇтьс¤. Ќа практиц≥ значенн¤ t, ¤к правило, лежить в межах в≥д 7 до 10. якщо матриц¤ ¬ розкладаЇтьс¤, то це св≥дчить або про помилки в п≥дбор≥ експерт≥в, або про њхн≥ серйозн≥ розб≥жност≥. ¬ обох випадках доц≥льно зм≥нити склад експертноњ ком≥с≥њ.
јнал≥з компетентност≥ експерт≥в за њхн≥ми оц≥нками. омпетентн≥сть експерта може бути оц≥нена на п≥дстав≥ р≥вн¤ погодженост≥ його оц≥нки з оц≥нками б≥льшост≥ експерт≥в.
Ќехай отримано матрицю в≥дносних експертних оц≥нок S=(sij), i = 1, Е, n, j=1, Е, m, де sij Ц в≥дносна оц≥нка ≥-тоњ функц≥њ, надана j-м експертом. “од≥ дл¤ (n x m) - вим≥рноњ матриц≥ експертних оц≥нок S формула розрахунку n - вим≥рного вектора S та m - м≥рного вектора q маЇ такий вигл¤д [166]:
 , t=1,
2, Е ,
(4.17)
, t=1,
2, Е ,
(4.17)
де qo = (1/m, Е, 1/m) Ц m - вим≥рний вектор початкових коеф≥ц≥Їнт≥в експерт≥в;
![]() - Ї сумою
компонент вектора st
S.
- Ї сумою
компонент вектора st
S.
«ауважимо, що stS=STst, де ≥ндексом “ позначено операц≥ю транспонуванн¤ матриць, тобто дл¤ елемент≥в матриц≥ S Ї справедливим
s![]() = sji
= sji
«важаючи на це, р≥вн¤нн¤ (4.17) можна
перетворити:
st
= S![]() =
S
=
S![]() st-1
S
=
st-1
S
=![]() SSTst-1
, qt
=
SSTst-1
, qt
= ![]() stS
=
stS
= ![]() STqt-1S
STqt-1S
=
![]() STSqt-1
. ќтже отримуЇмо:
st
=
STSqt-1
. ќтже отримуЇмо:
st
= ![]() SSTst-1;
qt =
SSTst-1;
qt = ![]() STqt-1.
STqt-1.
‘актично зд≥йснено перех≥д до рекуректних формул. р≥м того, обчисленн¤ за формулою (4.17) зводитьс¤ до паралельного зд≥йсненн¤ двох розрахунк≥в (4.16), у ¤ких зам≥сть матриц≥ ¬ фигурують ssT та sTs. ”мови зб≥жност≥ St i qt так≥ ж, ¤к ≥ у попередньому п. 3.2. ќск≥льки матриц¤ S Ї нев≥дТЇмною, то SST та STS також нев≥дТЇмн≥. ћи припускаЇмо, що матриц¤ S не розкладаЇтьс¤, тобто шл¤хом переставленн¤ р¤дк≥в ≥ (або) стовпчик≥в њњ неможна привести до вигл¤ду:
S
= ![]() ,
,
бо у супротивному випадку експерти розпод≥л¤ютьс¤ на дв≥ протилежн≥ групи, ≥ застосовувати методи, що розгл¤даютьс¤, не можливо.
√раничн≥ вектори s
= ![]() та q
=
та q
= ![]() Ї
в≥дпов≥дно власними векторами матриць SST
та STS,
що в≥дпов≥дають њхн≥м максимальним власним
числам. ѕри цьому s=Sq
,
оск≥льки
s
= lim st = lim (Sqt-1) =
S
lim
qt-1
= Sq.
Ї
в≥дпов≥дно власними векторами матриць SST
та STS,
що в≥дпов≥дають њхн≥м максимальним власним
числам. ѕри цьому s=Sq
,
оск≥льки
s
= lim st = lim (Sqt-1) =
S
lim
qt-1
= Sq.
4.
“епер, знаючи коеф≥ц≥Їнти компетентност≥
експерт≥в, можна обчислити групов≥
експертн≥ оц≥нки функц≥й (задач) маркетингу
за такою формулою:
Ri
= ![]() i=
1, Е, m,
де Ri
Ц групова експертна оц≥нка ≥-тоњ
задач≥ ћ≤—; sij
Ц оц≥нка ≥-тоњ
функц≥њ (задач≥),
i=
1, Е, m,
де Ri
Ц групова експертна оц≥нка ≥-тоњ
задач≥ ћ≤—; sij
Ц оц≥нка ≥-тоњ
функц≥њ (задач≥),
компетентност≥ j-го експерта, j=1, Е, m; m Ц к≥льк≥сть експерт≥в.
ќтже, групов≥ експертн≥ оц≥нки функц≥й (задач) маркетингу отримуютьс¤ з ≥ндив≥дуальних за допомогою зважуванн¤ њх з обчисленими коеф≥ц≥Їнтами компетентност≥ експерт≥в.
”пор¤дкувавши отриман≥ групов≥ оц≥нки за спаданн¤м Ri1, Ri2, Е, Rin, отримуЇмо посл≥довн≥сть функц≥й (задач) ћ≤—, в котр≥й номера ≥1, ≥2, Е, ≥n показують пр≥оритет реал≥зац≥њ або автоматизац≥њ та впровадженн¤ функц≥й управл≥нн¤ ћ≤—.
« метою формуванн¤ типового перел≥ку задач (функц≥й) ћ≤— комерц≥йного банку доц≥льно, на наш погл¤д, застосувати вс≥ розгл¤нут≥ нами експертн≥ методи та ≥нтегральний метод ранжуванн¤ функц≥й. ѕроцес експертизи схематично можна описати таким чином. Ќаприклад, експертна група складаЇтьс¤ з трьох експерт≥в, ¤к≥ оц≥нювали пТ¤ть функц≥й ћ≤—: ‘1 Ц анал≥з стратег≥чних позиц≥й та виб≥р напр¤м≥в д≥¤льност≥; ‘2 Ц оц≥нка та анал≥з ¤кост≥ та конкурентоздатност≥ банк≥вського продукту; ‘3 Ц прогнозуванн¤ попиту на продукт; ‘4 Ц обл≥к та анал≥з виконанн¤ кредитних та ≥нших договор≥в; ‘5 Ц моделюванн¤ прийн¤тт¤ р≥шень при виведенн≥ на ринок нових продукт≥в.
«астосовуючи метод мед≥ани емен≥, експертами встановлено так≥ переваги функц≥й ћ≤—: 1-й експерт: ‘1>‘2>‘3>‘5>‘4; 2-й експерт: ‘3>‘1>‘5>‘2>‘4 ;
3-й
експерт: ‘1>‘3>‘5>‘2
![]() ‘4.
¬ цьому випадку вектори переваг будуть
такими: π(1) = (0;1;2;4;3) Ц дл¤ 1-го
експерта, π (2) = (1;3;0;4;2) Ц дл¤ 2-го
експерта, π (3) = (0;3;1;3;2) Ц дл¤ 3-го
експерта.
‘4.
¬ цьому випадку вектори переваг будуть
такими: π(1) = (0;1;2;4;3) Ц дл¤ 1-го
експерта, π (2) = (1;3;0;4;2) Ц дл¤ 2-го
експерта, π (3) = (0;3;1;3;2) Ц дл¤ 3-го
експерта.
ћатриц¤ втрат (rij), i=1, Е, 5; j=1, Е, 5, буде мати такий вигл¤д:
rij
= 
–озвТ¤завши задачу про призначенн¤ (4.11) - (4.14) з такими коеф≥ц≥Їнтами матриць втрат, отримаЇмо ранжуванн¤: ‘1>‘3>‘5>‘2>‘4. «астосуванн¤ експертами методу м≥н≥м≥зац≥њ в≥дхилень м≥ж перевагою групи та ≥ндив≥дуальними р≥шенн¤ми привело до таких результат≥в. ≤ндив≥дуальн≥ переваги функц≥й, виражен≥ в балах, подан≥ в табл. 4.4, а матриц¤ розб≥жностей оц≥нок експерт≥в та максимальн≥ розб≥жност≥ наведен≥ в табл. 4.5
“аблиц¤ 4. 4
≤ндив≥дуальн≥ переваги функц≥й банк≥вського маркетингу
|
‘ункц≥њ |
≥льк≥сть бал≥в |
||
|
1-й експерт |
2-й експерт |
3-й експерт |
|
| ‘1 | 5 | 4 | 5 |
| ‘2 | 4 | 2 | 2 |
| ‘3 | 3 | 5 | 4 |
| ‘4 | 2 | 1 | 1 |
| ‘5 | 1 | 3 | 3 |
≤ндив≥дуальн≥ переваги функц≥й банк≥вського маркетингу
ќтримане
таке ранжуванн¤ функц≥й маркетингу:
‘1>‘3>‘2>‘4![]() ‘5
‘5
“аблиц¤ 4.5
–озб≥жност≥ оц≥нок експерт≥в
|
ћатриц¤ розб≥жностей думок експерт≥в |
ћаксимальна розб≥жн≥сть |
||
| 0 | 1 | 0 | 1 |
| 1 | 3 | 3 | 3 |
| 2 | 0 | 1 | 2 |
| 3 | 4 | 4 | 4 |
| 4 | 2 | 2 | 4 |
“рет≥й метод, ¤кий пол¤гав у застосуванн≥ процедури анал≥зу п≥дсумк≥в бальноњ оц≥нки функц≥й з врахуванн¤м компетентност≥ експерт≥в, надав так≥ результати.
ѕ≥дсумки бальноњ оц≥нки функц≥й експертами записан≥ в табл.4.6.
“аблиц¤ 4.6
ѕ≥дсумки бальноњ оц≥нки функц≥й банк≥вського маркетингу
|
‘ункц≥њ |
Ѕали |
||
|
1-й експерт |
2-й експерт |
3-й експерт |
|
| ‘1 | 50 | 30 | 25 |
| ‘2 | 20 | 30 | 20 |
| ‘3 | 40 | 40 | 50 |
| ‘4 | 10 | 10 | 15 |
| ‘5 | 20 | 20 | 25 |
| —ума Sj | 140 | 130 | 135 |
ќбчислимо в≥дносн≥ оц≥нки важливост≥ ≥-тоњ
функц≥њ (≥=1, Е, 5) за висновком j-го
експерта (j=1, 2, 3) ≥ запишемо у вигл¤д≥
матриц≥ S![]() .
.
. S![]() =
=

Ѕальн≥ оц≥нки експерт≥в, проставлен≥ особою, в≥дпов≥дальною за проведенн¤ експертизи, за трьома критер≥¤ми ≥ 5-бальною шкалою надан≥ в табл.4.7.
“аблиц¤ 4.7
Ѕальн≥ оц≥нки експерт≥в за критер≥¤ми
|
ритер≥њ |
ќц≥нки, надан≥ |
||
| 1-м експертом |
2-м експертом |
3-м експертом |
|
|
вал≥ф≥кац≥¤ |
5 | 4 | 5 |
|
ќбТЇктивн≥сть |
4 | 4 | 3 |
|
—таж роботи |
3 | 5 | 3 |
|
—ума ћj |
12 | 13 | 11 |
—ума оц≥нок компетентност≥ вс≥х експерт≥в ћ дор≥внюЇ 36. «а формулою (4.15) обчислюЇмо в≥дносн≥ оц≥нки компетентност≥ q1=0,333 ; q2=0,362; q3=0,305. ƒал≥ розраховуЇмо групов≥ експертн≥ оц≥нки з врахуванн¤м компетентност≥ експерт≥в: R1=0,2578; R2=0,1761; R3=0,4957; R4=0,0853; R5=0,1596. “аким чином, отримане таке ранжуванн¤: ‘3>‘1>‘2>‘5>‘4.
≤нтегральний метод ранжуванн¤ передбачаЇ зведенн¤ результат≥в розгл¤нутих метод≥в (в третьому метод≥ дл¤ кращоњ наочност≥ оц≥нки помножен≥ на 10 ≥ округлен≥) ( табл.4.8).
“аблиц¤ 4.8
≤нтегральний метод ранжуванн¤
|
ћетоди |
‘ункц≥њ |
||||
| ‘1 | ‘2 | ‘3 | ‘4 | ‘5 | |
|
ћетод 1 (ранг) |
5 | 2 | 4 | 1 | 3 |
|
ћетод 2 (ранг) |
5 | 3 | 4 | 2 | 2 |
|
ћетод 3 (оц≥нка) |
2,6 | 1,8 | 3,2 |
0,9 |
1,6 |
¬икористовуючи (4.8), (4.9) ≥ припускаючи, р≥внозначн≥сть вс≥х метод≥в, отримуЇмо так≥ значенн¤ ≥нтегральних показник≥в: р1=0,91; р2=0,52; р3=0,81; р4=0; р5=0, 27
√раф≥чну ≥люстрац≥ю ранжуванн¤ функц≥й зображено на рис.4.4.

–ис.4.4. ƒ≥аграма ранжуванн¤ функц≥й ћ≤— комерц≥йного банку
ќтже, за допомогою даного методу маЇмо наступне ранжуванн¤ функц≥й: ‘1>‘3>‘2>‘5>‘4.
ѕроведен≥ досл≥дженн¤ щодо побудови функц≥ональноњ частини ћ≤— з використанн¤м розгл¤нутих вище метод≥в дозволили нам сформувати типовий перел≥к першочергових задач (автоматизованих функц≥й управл≥нн¤) (табл.4.9).
«г≥дно з концепц≥Їю маркетингу та прийн¤тою методолог≥Їю структуризац≥њ ћ≤— нами виокремлено с≥м взаЇмоповТ¤заних функц≥ональних п≥дсистем, хоча привТ¤зуванн¤ функц≥й (задач) до п≥дсистем не завжди Ї однозначним ≥ обовТ¤зковим.
“аким чином, використанн¤ методик структуризац≥њ ћ≤— та р≥зних метод≥в, моделей вибору автоматизац≥њ функц≥й (задач) маркетингу дозвол¤Ї сформувати наб≥р задач управл≥нн¤ в склад≥ ћ≤— будь-¤кого банку (табл.4.9).
ѕ≥д час розвитку системи ≥ банку функц≥ональна структура ћ≤—, зрозум≥ло, може бути доповнена новими задачами.
ћаючи функц≥ональну структуру ћ≤— ≥ знаючи трудом≥стк≥сть виконанн¤ управл≥нських функц≥й, можна реорган≥зувати ≥снуючу або створити нову
“аблиц¤ 4. 9
ѕерел≥к першочергових задач маркетингу в склад≥ ћ≤— комерц≥йного банку
|
ѕ≥дсистеми |
Ќайменуванн¤ задач (комплекс≥в задач) |
|
ƒосл≥дженн¤ ринку |
1. ќц≥нка ≥ прогнозуванн¤ попиту на банк≥вський продукт (комплекс моделей). 2. ¬изначенн¤ ≥ прогнозуванн¤ м≥сткост≥ ринку банк≥вських ѕродукт≥в. 3. –озрахунок ≥ прогнозуванн¤ частки ринку. 4. ¬иб≥р ≥ перегл¤д ринк≥в банк≥вських продукт≥в на баз≥ к≥льк≥сних оц≥нок. 5. ќптим≥зац≥¤ вибору сегмент≥в ринку дл¤ конкретного банк≥вського продукту. 6. ¬еденн¤ дов≥дкових баз даних ринковоњ конТюнктури. |
|
ѕродуктова пол≥тика |
1. ќц≥нка стратег≥чних позиц≥й ≥ виб≥р напр¤м≥в д≥¤льност≥. 2. ѕозиц≥юванн¤ банк≥вських продукт≥в на р≥зних ринках збуту. 3. ‘ормуванн¤ оптимальноњ виробничоњ програми (комплекс ћоделей.) 4. ќц≥нка ¤кост≥ та конкурентоздатност≥ банк≥вського продукту. 5. јнал≥з життЇвого циклу продукту. 6. омплекс задач п≥дтримки прийн¤тт¤ р≥шень щодо освоЇнн¤ нових банк≥вських продукт≥в. |
|
÷≥ноутворенн¤ |
1. –озрахунок базовоњ ц≥ни банк≥вського продукту (комплекс моделей). 2. ¬≥дстеженн¤ динам≥ки ц≥н на банк≥вський продукт за ринками збуту. 3. ѕрогнозуванн¤ ц≥н на банк≥вськ≥ продукти. |
|
—тимулюванн¤ збуту |
1. ќптим≥зац≥¤ розпод≥лу бюджета маркетингу. 2. ѕлануванн¤ бюджету рекламноњ компан≥њ. 3. ќбл≥к, оц≥нка, анал≥з ефективност≥ рекламноњ компан≥њ. 4. ќптим≥зац≥¤ вибору засоб≥в реклами. |
|
—тратег≥¤ в сфер≥ систем доставки |
1. ¬изначенн¤ оптимальних систем доставки. 2. јнал≥з розм≥щенн¤ точок збуту банк≥вських продукт≥в. 3. ѕрогнозуванн¤ ≥ плануванн¤ обс¤г≥в збуту банк≥вських продукт≥в. |
|
—тратег≥¤ ризику |
1. ќц≥нка конкретного виду ризику. 2. ¬становленн¤ оптимального р≥вн¤ ризику. 3. јнал≥з метод≥в зниженн¤ ризик≥в (кредитного, в≥дсоткового, ринкового, валютного) |
| ‘ормуванн¤ ≥ контроль маркетингових програм |
1. ‘ормуванн¤ бюджета маркетингу. 2. –озробка маркетингових програм. 3. онтроль виконанн¤ маркетингових програм. |
орган≥зац≥йну структуру управл≥нн¤ банку, що в≥дпов≥даЇ поставлен≥й мет≥.
ѕобудова ћ≤— повТ¤зана з≥ значними витратами творчоњ прац≥ ≥ грошових кошт≥в, проте без на¤вност≥ такоњ системи банк не може усп≥шно функц≥онувати ≥ розвиватис¤. –екомендуЇтьс¤ залучати до проектуванн¤ системи њњ майбутн≥х користувач≥в. олектив розробник≥в може складатис¤ ¤к ≥з фах≥вц≥в ≥з сучасних ≥нформац≥йних технолог≥й, так ≥ представник≥в служби маркетингу, а також ≥нших в≥дд≥л≥в та управл≥нь банк≥в. Ѕажаним Ї залученн¤ до ц≥лей роботи квал≥ф≥кованих експерт≥в в галуз≥ ≥нформац≥йних систем та маркетингу.